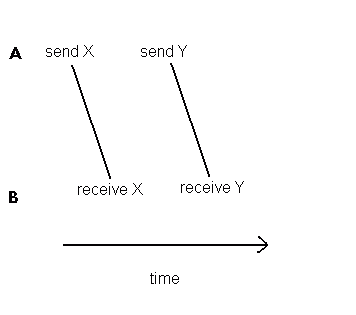This chapter has been excerpted from the book "Flow-Based Programming: A New Approach to Application Development" (van Nostrand Reinhold, 1994), by J.Paul Morrison. A second edition (2010) is now available from CreateSpace eStore and Amazon.com. The 2nd edition is also available in e-book format from Kindle (Kindle format) and Lulu (epub format). To find out more about FBP, click on FBP.
For definitions of FBP terms, see Glossary.
|
Material from book starts here:
In the middle years of this century, it was expected that eventually computers would be able to do anything that humans could explain to them. But even then, some people wondered how easy this would turn out to be. A book first published in the 1950's, "Faster than Thought" (Bowden 1963), contains the following remark:
"It always outrages pure mathematicians when they encounter commercial work for the first time to find how difficult it is." (p. 258)and further on:
"...it is so hard in practice to get any programme right that several mathematicians may be needed to look after a big machine in an office. ... It seems, in fact, that experienced programmers will always be in demand" (p. 259)
However, in those days, the main barrier was thought to be the difficulty of ascertaining the exact rules for running a business. This did turn out to be as hard as people expected, but for rather different reasons. Today we see that the problem is actually built right into the fundamental design principles of our basic computing engine - the so-called von Neumann machine we alluded to in Chapter 1.
The von Neumann machine is perfectly adapted to the kind of mathematical or algorithmic needs for which it was developed: tide tables, ballistics calculations, etc., but business applications are rather different in nature. As one example of these differences, the basic building block of programming is the subroutine, and has been since it was first described by Ada, Countess Lovelace, Lord Byron's daughter, in the last century [of course that is the 19th!] (quite an achievement, since computers did not exist yet!). This concept was solidly founded on the mathematical idea of a function, and any programmer today knows about a number of standard subroutines, and can usually come up with new ones as needed. Examples might include "square root", "binary search", "sine", "display a currency value in human-readable format", etc. What are the basic building blocks of business applications? It is easy to list functions such as "merge", "sort", "paginate a report", and so forth, but none of these seem to lend themselves to being encapsulated as subroutines. They are of a different nature - rather than being functions that operate at a single moment in time, they all have the characteristic of operating over a period of time, across a number (sometimes a very large number) of input and output items.
We now begin to get some inkling of what this difference might consist of. Business programming works with data and concentrates on how this data is transformed, combined and separated, to produce the desired outputs and modify stored data according to business requirements. Broadly speaking, whereas the conventional approaches to programming (referred to as "control flow") start with process and view data as secondary, business applications are usually designed starting with data and viewing process as secondary - processes are just the way data is created, manipulated and destroyed. We often call this approach "data flow", and it is a key concept of many of our design methodologies. It is when we try to convert this view into procedural code that we start to run into problems.
I am now going to approach this difference from a different angle. Let's compare a pure algorithmic problem with a superficially similar business-related one. We will start with a simple numeric algorithm: calculating a number raised to the 'n'th power, where 'n' is a positive, integer exponent. This should be very familiar to our readers, and in fact is not the best way to do this calculation, but it will suffice to make my point. In pseudocode, we can express this as follows:
/* Calculate a to the power b */
x = b
y = 1
do while x > 0
y = y * a
x = x - 1
enddo
return y
Figure 3.1
This is a very simple algorithm - easy to understand, easy to verify, easy to modify, based on well-understood mathematical concepts. Let us now look at what is superficially a similar piece of logic, but this time involving files of records, rather than integers. It has the same kind of structure as the preceding algorithm, but works with streams of records. The problem is to create a file OUT which is a subset of another one IN, where the records to be output are those which satisfy a given criterion "c". Records which do not satisfy "c" are to be omitted from the output file. This is a pretty common requirement and is usually coded using some form of the following logic:
read into a from IN
do while read has not reached end of file
if c is true
write from a to OUT
endif
read into a from IN
enddo
Figure 3.2
What action is applied to those records which do not satisfy our criterion? Well, they disappear rather mysteriously due to the fact that they are not written to OUT before being destroyed by the next "read". Most programmers reading this probably won't see anything strange in this code, but, if you think about it, doesn't it seem rather odd that it should be possible to drop important things like records from an output file by means of what is really a quirk of timing?
Part of the reason for this is that most of today's computers have a uniform array of pigeon-holes for storage, and this storage behaves very differently from the way storage systems behave in real life. In real life, paper put into a drawer remains there until deliberately removed. It also takes up space, so that the drawer will eventually fill up, preventing more paper from being added. Compare this with the computer concept of storage - you can reach into a storage slot any number of times and get the same data each time (without being told that you have done it already), or you can put a piece of data in on top of a previous one, and the earlier one just disappears.... Although destructive storage is not integral to the the von Neumann machine, it is assumed in many functions of the machine, and this is the kind of storage which is provided on most modern computers. Since the storage of these machines is so sensitive to timing and because the sequencing of every instruction has to be predefined (and humans make mistakes!), it is incredibly difficult to get a program above a certain complexity to work properly. And of course this storage paradigm has been enshrined in most of our higher level languages in the concept of a "variable". In a celebrated article John Backus (1978) actually apologized for inventing FORTRAN! That's what I meant earlier about the strange use of the equals sign in Higher Level Languages. To a logician the statement J = J + 1 is a contradiction (unless J is infinity?) - yet programmers no longer notice anything strange about it!
Suppose we decide instead that a record should be treated as a real thing, like a memo or a letter, which, once created, exists for a definite period of time, and must be explicitly destroyed before it can leave the system. We could expand our pseudo-language very easily to include this concept by adding a "discard" statement (of course the record has to be identified somehow). Our program might now read as follows:
read record a from IN
do while read has not reached end of file
if c is true
write a to OUT
else
discard a
endif
read record a from IN
enddo
Figure 3.3
Now we can reinterpret "a": rather than thinking of it as an area of storage, let us think of "a" as a "handle" which designates a particular "thing" - it is a way of locating a thing, rather than the storage area containing the thing. In fact, these data things should not be thought of as being in storage: they are "somewhere else" (after all, it does not matter where "read" puts them, so long as the information they contain becomes available to the program). These things really have more attributes than just their images in storage. The storage image can be thought of as rather like the projection of a solid object onto a plane - manipulating the image does not affect the real thing behind the image. Now a consequence of this is that, if we reuse a handle, we will lose access to the thing it is the handle of. This therefore means that we have a responsibility to properly dispose of things before we can reuse their handles.
Notice the difficulty we have finding a good word for "thing": the problem is that this is really a concept which is "atomic", in the sense that it cannot be decomposed into yet more fundamental objects. It has had a number of names in the various dialects of FBP, and has some affinities with the concept of "object" in Object-Oriented Programming, but I feel it is better to give it its own unique name. In what follows, we will be using the term "information packet" (or "IP"). IPs may vary in length from 0 bytes to 2 billion - the advantage of working with "handles" is that IPs are managed the same way, and cost the same to send and receive, independently of their size.
So far, we have really only added one concept - that of IPs - to the conceptual model we are building. The pseudo-code in Figure 3.3 was a main-line program, running alone. Since this main-line can call subroutines, which in turn can call other subroutines, we have essentially the same structure as a conventional program, with one main line and subroutines hung off it, and so on. Now, instead of just making a single program more complex, as is done in conventional programming, let us head off in a rather different direction: visualize an application built up of many such main-line programs running concurrently, passing IPs around between them. This is very like a factory with many machines all running at the same time, connected by conveyor belts. Things being worked on (cars, ingots, radios, bottles) travel over the conveyor belts from one machine to another. In fact, there are many analogies we might use: cafeterias, offices with memos flowing between them, people at a cocktail party, and so forth. After I had been working with these concepts for several years, I took my children to look at a soft-drink bottling plant. We saw machines for filling the bottles, machines for putting caps on them and machines for sticking on labels, but it is the connectivity and the flow between these various machines that ensures that what you buy in the store is filled with the right stuff and hasn't all leaked out before you purchase it!
An FBP application may thus be thought of as a "data factory". The purpose of any application is to take data and process it, much as an ingot is transformed into a finished metal part. In the old days, we thought that it would be possible to design software factories, but now we see that this was the wrong image: we don't want to mass-produce code - we want less code, rather than more. In hindsight it is obvious - it is the data which has to be converted into useful information in a factory, not the programs.
Now think of the differences between the characteristics of such a factory and those of a conventional, single main-line program. In any factory, many processes are going on at the same time, and synchronization is only necessary at the level of an individual work item. In conventional programming, we have to know exactly when events take place, otherwise things are not going to work right. This is largely because of the way the storage of today's computers works - if data is not processed in exactly the right sequence, we will get wrong results, and we may not even be aware that it has happened! There is no flexibility or adaptability. In our factory image, on the other hand, we don't really care if one machine runs before or after another, as long as processes are applied to a given work item in the right order. For instance, a bottle must be filled before it is capped, but this does not mean that all the bottles must be filled before any of them can be capped. It turns out that conventional programs are full of this kind of unnecessary synchronization, which reduces productivity, puts unnecessary strains on the programmers and generally makes application maintenance somewhere between difficult and impossible. In a real factory, unnecessary constraints of this sort would mean that some machines would not be utilized efficiently. In programming, it means that code steps have to be forced into a single sequence which is extremely difficult for humans to visualize correctly, because of a mistaken belief that the machine requires it. It doesn't!
An application can alternatively be expressed as a network of simple programs, with data travelling between them, and in fact we find that this takes advantage of developers' visual or "spatial" imagination. It is also a good match with the design methodologies generally referred to under the umbrella of Structured Analysis. The so-called "Jackson inversion model" (M. Jackson 1975) designs applications in this form, but then proposes that all the processes except one (the main-line) be "inverted" into subroutines. This is no longer necessary! Interestingly, Jackson starts off his discussion of program inversion with a description of a simple multiprogramming scheme, using a connection with a capacity of one (in our terminology). He then goes on to say, "Multi-programming is expensive. Unless we have an unusually favourable environment we will not wish to use the sledgehammer of multi-programming to crack the nut of a small structure clash." In FBP we have that "unusually favourable environment", and I and a number of other people believe he wrote off multi-programming much too fast!
How do we get multiple "machines" to share a real machine? That's something we have known how to do for years - we just give them slices of machine time whenever they have something to do - in other words, let them "time-share". In conventional programming, time-sharing was mostly used to utilize the hardware efficiently, but it turns out that it can also be applied to convert our "multiple main-line" model into a working application. There are a great many possible time-sharing techniques, but in FBP we have found one of the simplest works fine: we simply let one of our "machines" (called "processes") run until an FBP service request cannot be satisfied. When this happens, the process is suspended and some other ready process gets control. Eventually, the suspended process can proceed (because the blocking condition has been relieved) and will get control when time becomes available. Dijkstra called such processes "sequential processes", and explains that the trick is that they do not know that they have been suspended. Their logic is unchanged - they are just "stretched" in time.
Now you may have guessed that the FBP service requests we referred to above have to do with communication between processes. Processes are connected by means of FIFO (first-in, first-out) queues or connections which can hold up to some maximum number of IPs (called a queue's "capacity"). For a given queue, this capacity may run from one to quite large numbers. Connections use slightly different verbs from files, so we will convert the pseudocode in the previous example, replacing:
-
"read" with "receive"
-
"write" with "send"
-
"discard" with "drop"
-
"end of file" with "end of data"
A "receive" service may get blocked because there is no data currently in the connection, and a "send" may be blocked because the connection is full and cannot accept any more data for a while. Think of a conveyor belt with room for just so many bottles, televisions, or whatever: it can be empty, full or some state in between. All these situations are normally just temporary, of course, and will change over time. We have to give connections a maximum capacity, not only so that our applications will fit into available storage, but also so that all data will eventually be processed (otherwise data could just accumulate in connections and never get processed).
Now processes cannot name connections directly - they refer to them by naming ports, the points where processes and connections meet. More about ports later.
The previous pseudocode now looks like this:
receive from IN using a
do while receive has not reached end of data
if c is true
send a to OUT
else
drop a
endif
receive from IN using a
enddo
Figure 3.4
I deliberately used the word "using" on the "receive" to stress the nature of "a" as a handle, but "send a" seems more natural than "send using a". Note the differences between our file processing program and our FBP component:
-
differences in the verbs (already mentioned)
-
IPs "out there", rather than records in storage
-
IPs must be positively disposed of
-
port names instead of file names.
We said earlier that IPs are things which have to be explicitly destroyed - in our multi-process implementation, we require that all IPs be accounted for: any process which receives an IP has its "number of owned IPs" incremented, and must reduce this number back to zero before it exits. It can do this in essentially the same ways we dispose of a memo: destroy it, pass it on or file it. Of course, you can't dispose of an IP (or even access it) if you don't have its handle (or if its handle has been reused to designate another IP). Just like a memo, an IP cannot be reaccessed by a process once it has been disposed of (in most FBP implementations we zero out the handle after disposing of the IP to prevent exactly that from happening).
To get philosophical for a moment, proponents of "garbage collection" tend to feel that IPs should disappear when nobody is looking at them (no handles reference them), but the majority of the developers of FBP implementations felt that that was exactly what was wrong with conventional programming: things could disappear much too easily. So we insisted that a process get rid of all of its IPs, explicitly, one way or another, before it gives up control. If you inject an IP in at one end of the network, you know it is going to get processed unless or until some process explicitly destroys it! Conversely, if you build a table IP, and forget to drop it when you are finished, many people might argue that it would be nice to have the system dispose of it for you. On the other hand... I could argue that such an error (if it is an error) may be a sign of something more fundamentally wrong with the design or the code. And anyway, all recent FBP implementations detect this error, and list the IPs not disposed of, so it is easy to figure out what you did wrong. So..., if we can do that, why not let garbage collection be automatic? Well, our team took a vote, and strict accounting won by a solid majority! It might have lost if the group had had a different composition! Eventually, we could make this both an environmental decision and an attribute of each component, so we could detect if a "loose" component was being run in a "tight" shop.
Now what are "IN" and "OUT" that our pseudocode receives IPs from and sends them to? They are not the names of connections, as this would tie a component's code to one place in the network, but are things called "ports". "Portae" means "gates" in Latin, and ports (like seaports) can be thought of as specific places in a wall or boundary where things or people go in or out. Weinberg (1975) describes a port as
"... a special place on the boundary through which input and output flow... Only within the location of the port can the dangerous processes of input and output take place, and by so localizing these processes, special mechanisms may be brought to bear on the special problems of input and output."
Now doors have an "inside" aspect and an "outside" aspect - the name of the inside aspect might be used by people inside the house to refer to doors, e.g. "let the cat out the side door", while the outside aspect is related to what the door opens onto, and will be of interest to city planners or visitors. Ports in FBP have the same sort of dual function: they allow an FBP component to refer to them without needing to be aware of what they open onto. Port names establish a relationship between the receives and sends inside the program and program structure information defined outside the component. This somewhat resembles subroutine parameters, where the inside (parameters) and the outside (arguments) have to correspond, even though they are compiled separately. In the case of parameters, this correspondence is established by means of position (sequence number). In fact, in AMPS and DFDM ports were identified by numbers rather than by names. While this convention gives improved performance by allowing ports to be located faster, our experience is that users generally find names easier to relate to than numbers - just as we say "back door" and "front door", rather than "door 1", "door 3", etc. For this reason, THREADS uses port names, not numbers.
Some ports can be defined to be arrays, so that they are referenced by an index as well as a name. Thus, instead of sending to a single OUT port, some components can have a variable number of OUT ports, and can therefore say "send this IP to the first (or n'th) OUT port". This can be very useful for components which, say, make multiple copies of a given set of information. The individual slots of an array-type port are called "port elements". Naturally you can also have array-type ports as input ports, which might for instance be used in components which do various kinds of merge operation. Finally, a method is provided for the component to find out how many elements of an array-type port are connected, and which ones. In DFDM we did not need array-type ports as ports were numbered, so you could define, say, ports 3 to 20 as acting as a single array.
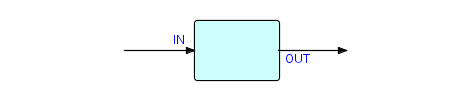
Now let's draw a picture of the component we built above. It's
called
a "filter" and looks like this:
Figure 3.5
This component type has a characteristic "shape", which we will encounter frequently in what follows. FBP is a graphical style of programming, and its usability is much enhanced by (although it does not require) a good picture-drawing tool. Pictures are an international language and we have found that FBP provides an excellent medium of communication between application designers and developers and the other people in an organization who need to be involved in the development process.
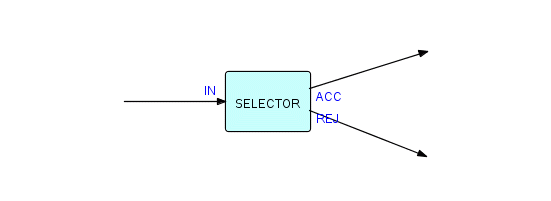
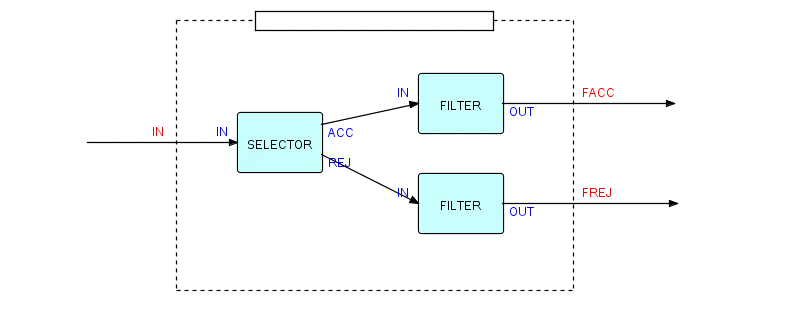
Now we will draw a different shape of component, called a "selector". Its function is to apply some criterion "c" to all incoming IPs (they are received at port IN), and send out the ones that match the specified criterion to one output port (ACC), while sending the rejected ones to the other output port (REJ). Here is the corresponding picture:
Figure 3.6
You will probably have figured out the logic for this component yourself. In any case, here it is:
receive from IN using a
do while receive has not reached end of data
if c is true
send a to ACC
else
send a to REJ
endif
receive from IN using a
enddo
Figure 3.7
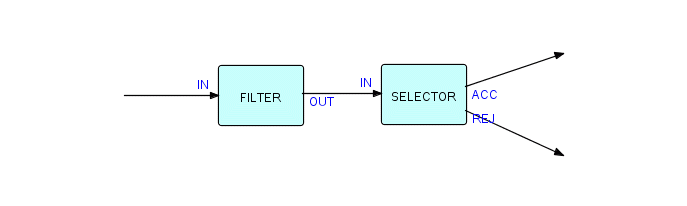
Writing components is very much like writing simple main-line programs. Things really get interesting when we decide to put them together. Suppose we want to apply the filter to some data and then apply the selector to the output of the filter: all we need to record is that, for this application, OUT of FILTER is connected to IN of SELECTOR. You will notice that IN is used as a port name by both FILTER and SELECTOR, but this is not a problem, as port names only have to be unique within a given component, not across an entire application.
Let us draw this schematically:
Figure 3.8
We have just drawn our first (partial) FBP structure! FBP software can execute this kind of diagram directly (without our having to convert it to procedural code), and in fact you can reconfigure it in any way you like - add components, remove them, rearrange them, etc., endlessly. This is the famous "Legoland programming" which we have all been waiting for!
Now what is the line marked "C" in the diagram? It is the connection across which IPs will travel when passing from FILTER to SELECTOR. It may be thought of as a pipe which can hold up to some maximum number of IPs (its "capacity"). So to define this structure we have to record the fact that OUT of FILTER is connected to IN of SELECTOR by means of a connection with capacity of "n".
Now how do we prove to our satisfaction that this connection is processing our data correctly? Well, there are two constraints that apply to IPs passing between any two processes. If we use the names in the above example, then:
-
every IP must arrive at SELECTOR after it leaves FILTER
-
any pair of IPs leaving FILTER in a given sequence must arrive at SELECTOR in the same sequence
The first constraint is called the "flow" constraint, while the second is called the "order-preserving" constraint. If you think about it using a factory analogy, this is all you need to ensure correct processing. Suppose two processes A and B respectively generate and consume two IPs, X and Y. A will send X, then send Y; B will receive X, then receive Y (order-preserving constraint). Also, B must receive X after A sends it, and similarly for Y (flow constraint). This does not mean that B cannot issue its "receives" earlier - it will just be suspended until the data arrives. It also does not matter whether A sends Y out before or after B receives X. The system is perfectly free to do whatever results in the best performance. We can show this schematically - clearly the second diagonal line can slide forward or back in time without affecting the final result.
Figure 3.9
Connections may have more than one input end, but they may only have one output. IPs from multiple sources will merge on a connection, arriving at the other end in "first come, first served" sequence. It can be argued that by allowing this, we lose the predictability of the relationship between output and input, but it is easy enough to put a code in the IPs if you ever want to separate them again.
Up to now, we have been ignoring where IPs come from originally. We have talked about receiving them, sending them and dropping them, but presumably they must have originally come into existence at some point in time. This very essential function is called "create" and is the responsibility of whichever component first decides that an IP is needed. The "lifetime" of an IP is the interval between the time it is created and the time it is destroyed. From one point of view it is obvious that something needs to be created before it can be used, but how does this apply to a business application? Well, a lot of the IPs in an application are created from file records: generally file records are turned into IPs at file reading time, and the IPs are turned back into file records (and then destroyed) at file writing time. There are two standard components to do these functions (Read Sequential and Write Sequential), which we will talk more about in succeeding chapters. However, it often happens that you decide to create a brand new IP for a particular purpose which may never appear on a file - one example of these are the "control IPs" which we will describe in a later chapter. Another example might be a counting component which counts the IPs it receives, using a "counter" IP. This IP is used to maintain the count, and is finally sent to the output port when the counter terminates. Such a component will receive the IPs being counted, but, before it starts counting, it has to create a counter IP in which the count is to be maintained.
This is the typical logic of a Counter component (by the way, this kind of component normally tries to send incoming IPs to an output port, and drops them if this port is not connected):
create counter IP using c
zero out counter field in counter IP
receive from IN using a
do while receive has not reached end of data
increment count in counter IP
send a to OUT
if send wasn't successful,
drop a
endif
receive from IN using a
enddo
send c to COUNT port
Figure 3.10
To discover whether OUT is connected, we simply try to send to this port. If the send works, the IP is disposed of; if not, we still have it, so we dispose of it by dropping it. What if COUNT is not connected? Since the whole point of this component is to calculate a count, if COUNT is not connected there's not much point in even running this component, so it would be even better to test this right up front.
As we said above, all IPs must eventually be disposed of, and this will be done by some function which knows that the IP in question is no longer needed. This will often be Writer components, but not necessarily. The Selector example above should really be enhanced as follows:
receive from IN using a
do while receive has not reached end of data
if c is true
send a to ACC
else
send a to REJ
endif
if the send wasn't successful,
drop a
endif
receive from IN using a
enddo
Figure 3.11
At the beginning of this chapter, we talked about data as being primary. In FBP it is not file records which are primary, but the IPs passing through the application's processes and connections. Our experience is that this is almost the first thing an FBP designer must think about. Once you start by designing your IPs first, you realize that file records are only one of the ways a particular process may decide to store IPs. The other thing file records are used for is to act as interfaces with other systems, but even here they still have to be converted to IPs before another process can handle them.
Let's think about the IPs passing across any given connection - what is their layout? Clearly it must be something that the upstream process can output and the downstream process can handle. The FBP methodology requires the designer to lay out the IPs first, and then define the transforms which apply to them. If two connected components have different requirements for their data, it is simple to insert a "transform" component between them. The general rule is that two neighbours must either agree on the format of data they share, or agree on data descriptions which encode the data format in some way. Suppose, for instance, that process B can handle two formats of IP. If the application designer knows that process A is always going to generate the first format, s/he may parametrize B so that it knows what to expect. If A is going to generate an unpredictable mix of the two formats, it will have to indicate to B for each IP what format it is in, e.g. by an agreed-upon code in a field, by IP length, by a preceding IP, or whatever. An interesting variant of this is to use free-form data. There may be situations where you don't want to tie the format of IPs down too tightly, e.g. when communicating between subsystems which are both undergoing change. To separate the various fields or sections, you could imbed delimiters into the data. You will pay more in CPU time, but this may well be worth it if it will reduce your maintenance costs. This is why, for instance, communication formats between PCs and hosts often use free-form ASCII separated by delimiters (binary fields present unique problems when uploading and downloading data). Lastly, the more complete FBP implementations provide mechanisms for attaching standard descriptions to IPs, called Descriptors, allowing them to be used and reused in more and more applications. Descriptors allow individual fields in IPs to be retrieved or replaced by name - I will be describing them in more detail in a later chapter.
The next concept I want to describe is the ability to group components into packages which can be used as if they were components in their own right. This kind of component is called a "composite component". It is built up out of lower-level components, but on the outside it looks just like any other component. Components which are not built up of lower-level components are called "elementary", and are usually written in some Higher Level Language (DFDM supports both PL/I and VS COBOL II), while THREADS supports C. DFDM as distributed also includes a small set of "starter set" components written in a low-level programming language for performance reasons, but it is not expected that the majority of users will need to code at this level.
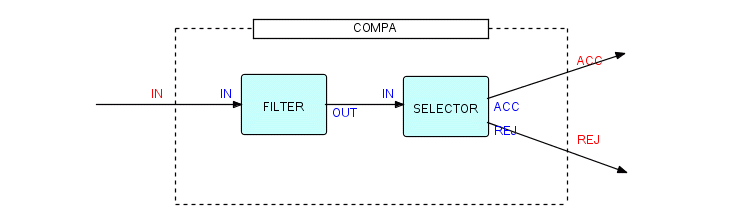
To make a composite component look like other components from the outside, obviously it must have ports of its own. We will therefore take the previous diagram, and show how we can package it into a composite called COMPA:
Figure 3.12
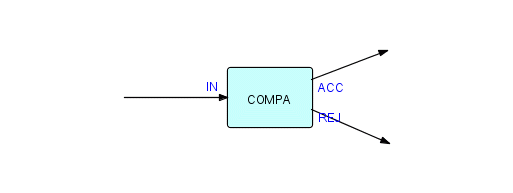
Once we have done this, COMPA can be used by anyone who knows what formats of data may be presented at port IN of COMPA and what formats will be sent out of its ACC and REJ ports. You will notice that it is quite acceptable for our composite to have the same port names as one of its internal components. You might also decide to connect the ACC port inside to the REJ port outside, and vice versa - what you would then have is a Rejector composite process, rather than an Acceptor. Of course COMPA is not a very informative name, and in fact we probably wouldn't bother to make this function a composite unless we considered it a useful tool which we expected to be able to reuse in the future.
Notice also that we have shown the insides of COMPA - from the outside it looks like a regular component with one input port and two output ports, as follows:
Figure 3.13
Now, clearly, any port on a composite must have corresponding ports "on the inside". However, the inverse is not required - not all ports on the inside have to be connected on the outside - if an inside component tries to send to an unconnected composite port, it will get a return of "unconnected" or "closed", depending on the implementation.
We have now introduced informally the ideas of "port", "connection", "elementary component", "composite component" and "information packet".
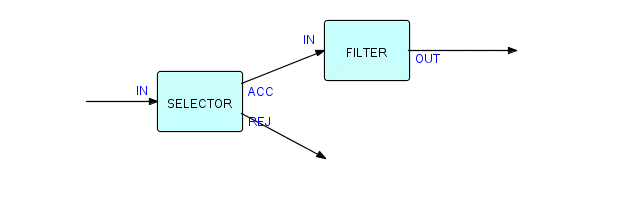
At this point, we should ask: just what are the things we are connecting together? We have spoken as though they were components themselves, but actually they are uses or occurrences of components. There is no reason why we cannot use the same component many times in the same structure. Let us take the above structure and reverse it. We then get the following:
Figure 3.14
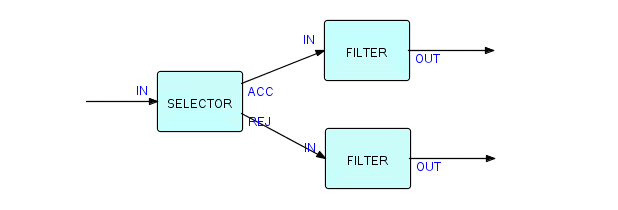
Let's attach another FILTER to the REJ port of SELECTOR. Now the picture looks like this:
Figure 3.15
Here we have two occurrences of the FILTER component running concurrently, one "filtering" the accepted IPs from SELECTOR, the other filtering the rejected ones. This is no different from having two copiers in the same office. If we have only one copier, we don't have to identify it further, but if we have more than one, we have to identify which one we mean by describing them or labelling them - we could call one "the big copier" and the other "the little copier", or "copier A" and "copier B". In DFDM we took the function name and qualified it - in THREADS we make what might be called the "in context" function the name, and qualify it to indicate which component we are using. These component occurrences are called processes, and it is time to explain this concept in more depth.
In conventional programming, we talk about a program "performing some function", but actually it is the machine which does the function - the program just encodes the rules the machine is to follow. In conventional programming, much of the time we do not have to worry about this, but in FBP (as also in operating system design and a number of other specialized areas of computing) we have to look a little more closely at this idea. In FBP, the different components are executed by the CPU in an interleaved manner, where the CPU gives time to each component in turn. Since you can have multiple occurrences of the same component, with each occurrence being given its own series of time slots and its own working storage, we need a term for the thing which the CPU is allocating time slices to - we call this a "process". The process is what the CPU "multithreads" (some systems distinguish between processes and threads, but we will only use the term "process" in what follows). Since multiple processes may execute the same code, we may find situations where the first process using the code gets suspended, the code is again entered at the top by another process, which then gets suspended, and then the first process resumes at the point where it left off. Obviously, the program cannot modify its own code (unless it restores the code before it can be used by another process), otherwise strange things may happen! In programming terms, the code has to be read-only. In IBM's MVS, this kind of program is called reentrant, which is not quite as stringent as read-only, but read-only implies reentrancy, and I have found that making code read-only is a good programming discipline, as it makes a clear distinction between variable data, on the one hand, and program code together with constants, on the other. Although this may sound arcane, it is not really that far removed from everyday life. Imagine two people reading a poster at the same time: neither of them needs to be aware of the point in the text the other one has reached. Either one of the readers can go away for a while and come back later and resume at the point where he or she left off, without interfering in the least with the other reader. This works because the poster does not change during the reading process. If, on the other hand, one person changes the poster while the other is trying to read it, they would have to be synchronized in some way, to prevent utter confusion on the part of the reader, at least.
We can now make an important distinction: composite components contain patterns of processes, not components. This becomes obvious when you think of a structure like the previous one - the definition of that composite has three nodes, but two of them are implemented by the same component, so they must be different processes. Of course, they don't become "real" processes until they actually run, but the nodes correspond one-to-one with processes, so they can be referred to as processes without causing confusion. Here is the same diagram shown as a composite:
Figure 3.16
When this composite runs, there will be three processes running in it, executing the code of two components.
Lastly, I would like to introduce the concepts of data streams and brackets. A "stream" is the entire series of IPs passing across a particular connection. Normally a stream does not exist all at the same time - the stream is continually being generated by one process and consumed by another, so only those IPs which can fit into the connection capacity could possibly exist at the same time (and perhaps not even that many). Think of a train track with tunnels at various points. Now imagine a train long enough that the front is in one tunnel while the end is still in the previous tunnel. All you can see is the part of the train on the track between the tunnels, which is a kind of window showing you an ever-changing section of the train. The IP stream as a whole is a well-defined entity (rather like the train) with a defined length, but all that exists at any point in time is the part traversing the connection. This concept is key to what follows, as it is the only technique which allows a very long stream of data to be processed using a reasonable amount of resources.
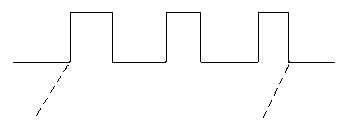
Just as an FBP application can be thought of as a structure of processes linked by connections, an application can also be thought of as a system of streams linked by processes. Up to now, we have sat on a process and watched the data as it is consumed or generated. Another, highly productive way of looking at your application is to sit on an IP and watch as it travels from process to process through the network, from its birth (creation) to its death (destruction). As it arrives at each process, it triggers an activity, much like the electrical signal which causes your phone to ring. Electrical signals are often shown in the textbooks like this:
trailing edge leading edge
Figure 3.17
The moment when the leading edge reaches something that can respond to it is an event. In the same way, every IP has both a data aspect and a control aspect. Not only is an IP a carrier of data, but its moment of arrival at a process is a distinct event. Some data streams consist of totally independent IPs, but most streams are patterns of IPs (often nested, i.e. smaller patterns within larger patterns) over time. As you design your application, you should decide what the various data streams are, and then you will find the processes falling out very naturally. The data streams which tend to drive all the others are the ones which humans will see, e.g. reports, etc., so you design these first. Then you design the processes which generate these, then the processes which generate their input, and so on. This approach to design might be called "output backwards"....
Clearly a stream can vary in size all the way from a single IP to many millions, and in fact it is unusual for all the IPs in the stream to be of the same type. It is much more common for the stream to consist of repeating patterns, e.g. the stream might contain multiple occurrences of the following pattern: a master record followed by 0 or more detail records. You often get patterns within patterns, e.g.
'm' patterns of:
city record, each one followed by
'n' patterns of:
customer record, each one followed by
'p' sales detail records for each customer
Figure 3.18
You will notice that this is in fact a standard hierarchical structure. The stream is in fact a "linearized" hierarchy, so it can map very easily onto (say) an IMS data base.
To simplify the processing of these stream structures, FBP uses a special kind of IP called a "bracket". These enable an upstream process to insert grouping information into the stream so that downstream processes do not have to constantly compare key fields to determine where one group finishes and the next one starts. As you might expect, brackets are of two types: "open brackets" and "close brackets". A group of IPs surrounded by a pair of brackets is called a "substream". In THREADS, we use IPs with "type" of "(" and ")" for open and close brackets, respectively.
We have one more decision to make before we can show how we might use brackets in the above example. We have two cases where a single IP of one type is followed by a variable number of IPs of a different type (or substreams). The question is whether the open bracket should go before the single IP or after it. In the former case, we might see the following (I'll use brackets to represent bracket IPs):
< city1
< cust11 detl111 detl112...>
< cust12 detl111 detl112...>>
< city2
< cust21 detl211 detl122...>
< cust22 detl221 detl222...>>
etc.
Figure 3.19
In the latter case, we would see:
city1 <
cust11 < detl111 detl112...>
cust12 < detl111 detl112...>>
city2 <
cust21 < detl211 detl122...>
cust22 < detl221 detl222...>>
etc.
Figure 3.20
From the point of view of processing, these two conventions are probably equivalent, but I tend to prefer the first one as it includes each customer IP in the same substream as its detail records, and similarly includes each city in the same substream as the customers that belong to that city. As of the time of writing, there is no strongly preferred convention, but you should make sure that all specifications for components which use substreams state which convention is being used. By the way, a very useful technique when processing substreams is the use of "control" IPs to "represent" a stream or substream. Both AMPS and THREADS and some of the versions of DFDM have the concept of a process-related stack, which is used to hold IPs in a LIFO sequence. In Chapter 9, I will be describing how these concepts can be combined.
We have now introduced the following concepts:
-
process
-
component (composite and elementary)
-
information packet (IP)
-
structure
-
connection
-
port and port element
-
stream
-
substream
-
bracket
Normally at this stage in a conventional programming manual we would leave you to start writing programs on your own. However, this is as unreasonable as expecting an engineer to start building bridges based on text-book information about girders and rivets. FBP is an engineering-style discipline, and there is a body of accumulated experience based on the above concepts, which you can and should take advantage of. Of course, you will develop your own innovations, which you will want to disseminate into the community of FBP users, but this will be built on top of the existing body of knowledge. You may even decide that some of what has gone before is wrong, and that is standard in an engineering-type discipline also. Isaac Newton said: "If I have seen further than other men, it is because I have stood on the shoulders of giants." Someone else said about (conventional, not FBP) programming: "We do not stand on their shoulders; we stand on their toes!" Programmers can now stop wearing steel-toed shoes!
Before we can see how to put these concepts together to do real work, two related ideas remain to be discussed: the design of reusable components and parametrization of such components (see the next chapter).