This chapter has been excerpted from the book "Flow-Based Programming: A New Approach to Application Development" (van Nostrand Reinhold, 1994), by J.Paul Morrison. A second edition (2010) is now available from CreateSpace eStore and Amazon.com. The 2nd edition is also available in e-book format from Kindle (Kindle format) and Lulu (epub format). To find out more about FBP, click on FBP.
For definitions of FBP terms, see Glossary.
|
Material from book starts here:
Deadlocks are one of the few examples in FBP of problems which cannot involve only one process, but arise from the interactions between processes. They occur when two or more processes interfere with each other in such a way that the network as a whole eventually cannot proceed. I know some programmers feel that they have traded the known difficulties of conventional programming for a new and exotic problem which seems very daunting, and they wonder if we have not just moved the complexity around! Although deadlocks may seem frightening at first, I can assure you that you will gain experience at recognizing network shapes which are deadlock-prone, and will learn reliable ways to prevent deadlocks from occurring. I know of no case where a properly designed network resulted in a deadlock during production.
First, however, I think we should look a little more deeply at the question I mentioned above: if FBP is as good as I claim, why does it give rise to a new and exotic class of problem which the programmer would not encounter in normal programming? Well, actually, it's not new - it's just that a conventional program has only one process, so you don't have to worry about deadlocks. In FBP we have multiple processes, and multiple processes have always given rise to deadlocks of various kinds. If I have convinced you in the foregoing pages that the FBP approach is worthwhile, then you will be relieved to know that there is quite a large literature on multi-process deadlocks. Anyone who has designed on-line or distributed systems has had to struggle with this concept. For instance, suppose two people try to access the same account at a bank through different Automatic Teller Machines (ATMs). In itself this doesn't cause a problem, one just has to wait until the other one is finished. Now suppose that they both decide to transfer money between the same two accounts, but in different directions. Normally, this would be programmed by having both transactions get both accounts in update mode (Get Hold in IMS DL/I terms). Now consider the following sequence of events (call the accounts X and Y):
-
trans A - get X with hold
-
trans B - get Y with hold
-
(1) trans B - try to get X with hold
-
(2) trans A - try to get Y with hold
At point (1), transaction B gets suspended because it wants X, which is held by A. At point (2), transaction A gets suspended because it wants Y, which is held by B. Now neither one can release the resource the other one wants. If A had not needed Y, it would have eventually finished what it was doing, and released X, so B could have proceeded. However, now that it has tried to grab Y, the result is an unbreakable deadlock. This is often referred to as a "deadly embrace", and in fact it has similarities to one kind of FBP deadlock. Usually on-line systems have some kind of timeout which will cancel one or both of the transactions involved.
Normally, the chance of this kind of thing happening is infinitesimal, so a lot of systems simply don't worry about it. It can be prevented completely by always getting accounts in a fixed sequence, but this may not possible in all situations, so it is probably true to say that some proportion (even if a tiny one) of transactions will deadlock in an on-line system, so you have to be able to take some kind of remedial action.
In FBP, we can also get deadlocks between the processes of a network. Of course, in an FBP on-line system, each transaction would be a network, so you can get deadly embraces between separate networks requesting the same resources, but we will assume these are handled in the normal way for the underlying resource management software. However, because a network has multiple processes, we can get deadlocks within a network. In all these intra-network cases, we have discovered that it is always a design issue.
This type of deadlock can always be detected at design time, and there are tried and true techniques for preventing them, which we will be talking about in this chapter. Wayne Stevens also has a very complete analysis of deadlocks and how to avoid them in Appendix B of his last book (Stevens 1991).
The general term for deadlocks like the deadly embrace is a "resource deadlock". There is a classical example of this in the literature called the "dining philosophers problem", which has been addressed by many of the writers on multiple processes. Imagine there is a table in a room, on which are are 5 chopsticks, spaced equally around the table, and a bowl of rice in the centre. When a philosopher gets hungry, he enters the room, picks up the two chopsticks on each side of his place, eats until satisfied and then leaves, replacing the chopsticks on the table (after cleaning them off, I hope). If all the philosophers go in at the same time, and each happens to pick up the chopstick to his right (or left), you get a deadlock, as nobody can eat, therefore nobody can free up a chopstick, therefore nobody can eat! Notice that the dining philosophers exhibit the same loop topology which I have been warning you about in earlier chapters. The dining philosophers can also suffer from the reverse syndrome, "livelock", where, even though there is no deadlock, paradoxically one of the philosophers is in danger of starving to death because there is no guarantee that he will ever get the use of two adjacent chopsticks. Kuse et al. (1986) proved that, although a network with fixed capacity connections (like the ones in FBP) can suffer from deadlock, it can never suffer from livelock.
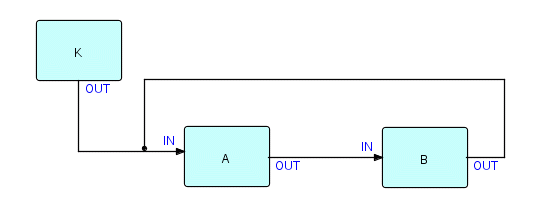
We will use Figure 14.2 from the chapter on Loop-Type Networks to introduce an FBP version of a resource deadlock. I'll show it again here for ease of reference:
Figure 16.1
Suppose that A's logic and B's logic are both the same, and look like this:
/* Copy IPs from IN to OUT */
receive from IN using a
do while receive has not reached end of data
send a to OUT
receive from IN using a
enddo
Figure16.2
In other words, they are both simple filters. However, suppose that under some circumstances B fails to send the IP it has just received to its OUT port, so its logic is effectively the following:
/* Copy c-type IPs from IN to OUT */
receive from IN using a
do while receive has not reached end of data
if condition c is true
send a to OUT
endif
receive from IN using a
enddo
Figure16.3
We'll begin by starting A. A sends an IP out of its OUT port. It next does a receive on IN, but there is nothing there, so it suspends. The connection between A and B now has something in it, so B starts up. Let's say condition "c" is false, so B receives the IP, but fails to send it out. B then goes on to its receive, and suspends. A is also suspended on a receive, but it is going to wait indefinitely as B hasn't sent the IP that A is waiting on. B is suspended indefinitely since A cannot send what B is waiting on. This is very like the deadly embrace: two processes, each suspended waiting for the other to do something. Since A and B are suspended on receive, there is nothing active in our network (K has terminated). So no process can proceed. The program as a whole has certainly not finished normally, but nothing is happening! This is in fact how the driver recognizes that a deadlock has occurred.
AMPS and DFDM add a wrinkle to this: it is possible to have one or more processes suspended waiting for an external event (such as I/O completion) to occur. In this case, the network as a whole goes into a "system wait", waiting on one or more external events. When one of these happens, the driver regains control, and gives control to the process in question. If it weren't for the fact that someone is waiting on an external event, this would look just like a deadlock. Instead, the event will eventually happen, allowing the process to continue, thus allowing all the other interlocked processes to start up as needed. This feature is one of the important performance advantages of FBP: unlike conventional programming, if a process needs to wait for an event to occur, it is usually not necessary with FBP to put the whole network into wait state (underlying software permitting).
Let's redraw the diagram with the states of each process shown in the top left corner of the process. You'll find this pattern of states is quite common, and is quite characteristic of a certain kind of deadlock. The drivers of all FBP implementations always list the process states as part of their diagnostic output in the event of a deadlock.
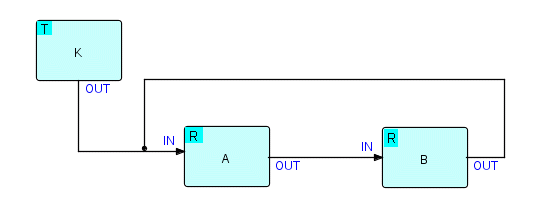
where T means terminated,
and R means suspended on receive
Figure16.4
Clearly, this kind of deadlock will occur any time a process outputs fewer IPs than the downstream process requires. Since the only kind of resource "native" to FBP is the IP, the only problem can be non-arrival of IPs. So thorough testing will detect it. We could also have "infrastructure" or "hybrid" (FBP plus infrastructure) deadlocks, where, say, one process is waiting on an external event which never happens, and another on an IP that the former is to send out. There is nothing to prevent a DFDM process from issuing an MVS ENQ, thus allowing two processes to interlock each other by both issuing two ENQs for the same resource, but in different orders. Old-style deadlock considerations apply here, but, as I've said, this is a well-understood area of computing.
The other class of deadlock familiar to systems programmers is the "storage deadlock". In this kind of deadlock, the deadlock occurs because one process does not have enough storage to store information which is going to be needed later. This type of deadlock, unlike the resource deadlock, can usually be resolved by providing more storage (not always, because some variants of this continually demand more storage...).
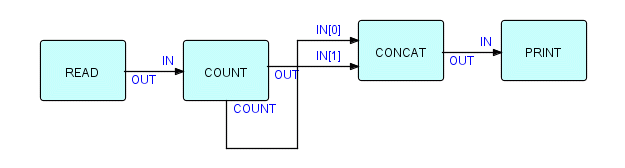
Here is an example of a storage deadlock: suppose you are counting a stream of IPs, and you want to print out all the IPs, followed by the count. The components for doing this should be quite familiar to you by now: the IPs to be counted go into the COUNT process at the IN port and emerge via the OUT port, while the count IP is generated and sent out via the COUNT port at close-down time. So all we have to do is concatenate the count IP after the ones coming from OUT. This is certainly very straightforward - here's the network:
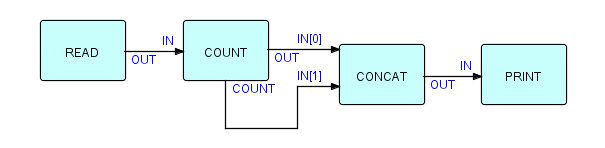
Figure16.5
We can code this up in THREADS, using the general purpose components available in THREADS. We will be describing the THREADS syntax more fully in Chapter 23 on "Notation", so we will not show the full network definition here, but the essential point is that we will connect the OUT port of Count to IN[0] of Concatenate, and the COUNT port of Count to IN[1] of Concatenate, as follows:
Read(THFILERD) OUT ->
IN Count(THCOUNT) OUT ->
IN [0] Concatenate(THMERGE) OUT ->
IN Print(THVIEW),
Count COUNT -> IN[1] Concatenate,
'data.fil' -> OPT Read;
Figure16.6
Running this network gives the following result, which is just what we would expect:
RUNNING NETWORK deadlk
Process: Read (THFILERD)
Connection: Read OUT[0] -> IN[0] Count
Process: Count (THCOUNT)
Connection: Count OUT[0] -> IN[0] Concatenate
Process: Concatenate (THMERGE)
Connection: Concatenate OUT[0] -> IN[0] Print
Process: Print (THVIEW)
Connection: Count COUNT[0] -> IN[1] Concatenate
IIP: -> OPT[0] Read
'data.fil'
Scan finished
Length: 3, Type: A, Data: 111
Length: 3, Type: A, Data: 123
Length: 3, Type: A, Data: 133
Length: 3, Type: A, Data: 134
Length: 3, Type: A, Data: 201
Length: 3, Type: A, Data: 211
Length: 3, Type: A, Data: 222
Length: 3, Type: A, Data: 234
Length: 3, Type: A, Data: 300
Length: 3, Type: A, Data: 450
Length: 3, Type: A, Data: 700
Length: 3, Type: A, Data: 999
Length: 10, Type: COUNT, Data: 12******70
Done
Figure16.7
In this example, the extra asterisks and 70 in the count IP are due to the fact that this particular Count component (THCOUNT) allocates a 10-character IP, but uses the C function "ltoa" to display the count, in this case resulting in 2 characters followed by a binary zero byte. The rest of the IP is unchanged, so it contains "garbage" (official programming term).
But now let's suppose that, for some perverse reason, you want to see the count IP ahead of the ones being counted. Since we're using a Concatenate function, you might think all we have to do is concatenate the count ahead of the IPs coming out of OUT. So we change the picture as follows:
Figure16.8
Let's change the previous network to do this and try it out:
Read(THFILERD) OUT ->
IN Count(THCOUNT) OUT ->
IN [1] Concatenate(THMERGE) OUT ->
IN Print(THVIEW),
Count COUNT -> IN[0] Concatenate,
'data.fil' -> OPT Read;
Figure16.9
To our surprise, the result of this is a little different:
RUNNING NETWORK deadlk
Process: Read (THFILERD)
Connection: Read OUT[0] -> IN[0] Count
Process: Count (THCOUNT)
Connection: Count OUT[0] -> IN[1] Concatenate
Process: Concatenate (THMERGE)
Connection: Concatenate OUT[0] -> IN[0] Print
Process: Print (THVIEW)
Connection: Count COUNT[0] -> IN[0] Concatenate
IIP: -> OPT[0] Read
'data.fil'
Scan finished
Deadlock detected
Process Print Not Initiated
Process Concatenate Suspended on Receive
Process Count Suspended on Send
Process Read Suspended on Send
Figure16.10
This is definitely not the result we wanted! Now, the message said "Deadlock", so, as before, let's try taking the process states and inserting them back into the diagram:
where S means suspended on send,
R means suspended on receive,
and N means not initiated
Figure16.11
You will find that in this kind of deadlock there is always a "bottleneck", or point where the upstream processes tend to be suspended on send, and the downstream processes are suspended on receive. As we saw before, some processes may have terminated - these can be excluded from this discussion. Processes which are inactive or not yet initiated can be treated as if they are suspended on receive.
If COUNT is suspended on send and CONCAT is suspended on receive, but they are adjacent processes, then clearly COUNT is sending data to a connection different from the one CONCAT is waiting on! Although there is data on the connection labelled OUT, CONCAT insists on waiting on a connection where there is no data, and, at this rate, there never will be! The problem is that the COUNT IP is not generated until all of the input IPs have been processed, and the connection labelled OUT has a limited capacity, so there is nowhere to store the IPs after they have been counted.
Although this kind of deadlock resembles a resource deadlock (because each process is waiting on the other to do something it can't do), it can be resolved by giving one or more connections more storage, so it is of the class of storage deadlocks. You will remember that we don't make all our queues "infinite" because then you can't guarantee that everything will get processed in a timely manner (or ever, if you want to allow 24-hour systems). But if you visualize the OUT connection bulging like a balloon as IPs are pumped into it, you can see that, eventually, COUNT is going to have processed all its input and will generate the count IP, and we can start to let the balloon deflate back to normal!
What's the best way of doing this? Unfortunately, the question depends on how many IPs are being counted. If you knew absolutely how many IPs there were, you could just make the capacity of the connection big enough. We can do this in THREADS by adding a capacity number in brackets after the arrow. Since "data.fil" has only 12 IPs, let's make the capacity 20:
Read(THFILERD) OUT ->
IN Count(THCOUNT) OUT -> (20)
IN [1] Concatenate(THMERGE) OUT ->
IN Print(THVIEW),
Count COUNT -> IN[0] Concatenate,
'data.fil' -> OPT Read;
Figure16.12
The result is as follows:
RUNNING NETWORK deadlk
Process: Read (THFILERD)
Connection: Read OUT[0] -> IN[0] Count
Process: Count (THCOUNT)
Connection: Count OUT[0] -> IN[1] Concatenate
Process: Concatenate (THMERGE)
Connection: Concatenate OUT[0] -> IN[0] Print
Process: Print (THVIEW)
Connection: Count COUNT[0] -> IN[0] Concatenate
IIP: -> OPT[0] Read
'data.fil'
Scan finished
Length: 10, Type: COUNT, Data: 12********
Length: 3, Type: A, Data: 111
Length: 3, Type: A, Data: 123
Length: 3, Type: A, Data: 133
Length: 3, Type: A, Data: 134
Length: 3, Type: A, Data: 201
Length: 3, Type: A, Data: 211
Length: 3, Type: A, Data: 222
Length: 3, Type: A, Data: 234
Length: 3, Type: A, Data: 300
Length: 3, Type: A, Data: 450
Length: 3, Type: A, Data: 700
Length: 3, Type: A, Data: 999
Done
Figure16.13
Worked like a charm!
Hold on, though - how do you know the file will never exceed 20 IPs? Remember the provinces of Canada - the process has already started which should eventually lead to the creation of a new one (or several). It's a fair bet that there will always be 7 days in a week, or 365 1/4 days in a year, but most other "constants" are subject to change, not to mention really variable numbers like the number of departments in a company.
Now suppose we follow the balloon analogy a bit further - what we could do is allow connections to bulge only if you would otherwise get a deadlock (i.e. no process can proceed), and let them bulge until we run out of storage. This initially seems attractive, but it makes error determination more complex. Remember that we allocate storage for IPs when they are created, not when we put them into a connection, so you will eventually run out of storage somewhere, and you won't know who is the culprit... And anyway, it's not a good idea to let the FBP Driver grab all of storage, because the storage some other subsystem needs to let it come down gracefully may not be available.
This whole area is tricky. If you know there will never be more than 50 provinces in Canada, and that you will never need more than 1000 bytes per province, you could hold them all in storage for a total of 50,000 bytes, which is pretty small peas these days. But what if each province is a tree, and you really don't know how many IPs are hung off each province, or how big they are?
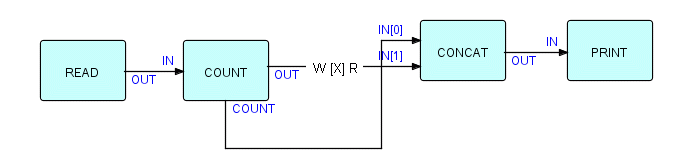
So far, the best general solution we have come up with is to use a sequential file. You will remember from Chapter 15 that we can replace any connection with a file. Let's change the network as follows, using the notation we used in Chapter 15:
Figure16.14
In that chapter we used ---W [X] R--- to indicate a "sandwich" with the file being the meat, and a Writer and Reader being the bread on each side. In Chapter 15, we used automatic ports to ensure that the Reader does not start until the Writer is finished.
Now, if you step this through in your head, or try it out on the machine, you will find that the file soaks up IPs until it gets end of data. Meanwhile CONCAT is waiting for data to arrive at IN[0]. The "meat" file's Reader can start at some point after this, but will only run until its output connection is full. At this point, the only thing that can happen is for CONCAT to receive the count IP, then end of data, then switch to receiving from IN[1]. From this point on, the data IPs will just flow through IN[1] to CONCAT's output port.
We have seen that you can set capacities on all connections. What would happen if we gave all connections a standard capacity of 10? Then examples like the above [the situation before we added the sequential file "sandwich"] would work fine as long as there were only 13 Canadian provinces and territories. Add another province one day, and your nice production program goes boom! Since amounts of test data tend to be smaller than production amounts, we would never be sure that programs which worked fine in test would not blow up in production. We have therefore adopted the strategy during testing of making connection capacities as small as possible, to prevent this kind of thing from happening. Zero-capacity connections would be very nice, but they are qualitatively different from non-zero-capacity connections (there are some situations where they really don't behave in the same way), so we use 1-capacity connections. Once we go into production, however, we can safely increase connection capacities to reduce context-switching overhead. This strategy has been followed in both DFDM and THREADS, and has been very successful at helping to reduce the occurrence of deadlocks. A propos, my son, Joseph Morrison, an experienced programmer, has suggested the following aphorism: "During testing, better to crash than to crawl; in production, better to crawl than crash!" The second half of this doesn't mean, of course, that you should put poorly performing systems into production - it just means that in production, when problems arise, it is better to try to keep going, even if in a degraded mode, but of course you should make sure someone knows what's going on! There is a story about one of the early computers (either SAGE or STRETCH) which did such a good job of correcting storage errors, that for some time nobody noticed that it was running slower and slower!
In Chapter 15, we talked about how the Writer/Reader sandwich is sometimes referred to as an "infinite queue". This is a general solution for storage deadlocks, and the only slightly tricky thing about such deadlocks is figuring out which connection has to be expanded. If you bear in mind that it must be a connection which is full (i.e. its upstream process is suspended on send) while its downstream process is suspended trying to receive from a different port, you'll find it pretty easily.
This dependency on number of IPs occurs in conventional programming, and you are probably familiar with the problem of having to make design decisions based on number of items. Michael Jackson [the writer on programming methodologies, not the singer] gives an example in his book (1975) of a file which consists of two types of groups of records (we would call them substreams), where the substream type is determined by the type of the last record, rather than the first. He gives as an example a file consisting of batches, each with a control record: if the control record agrees, you have a "good" batch; if it doesn't, it is a "bad" batch. The problem of course is: will the batch fit in storage? If it will fit safely, there's no problem. If not, you either use a file, or provide some form of backtracking (going ahead with your logic, but being prepared to undo some of it if it turns out to be a bad batch). In the foregoing I have tried to stress that it's not good enough if the batch fits into storage now - you have got to be sure it will fit in the future!
There is one final type of deadlock which again involves a loop-type network, but where most of the processes are suspended on send. This is more like a resource deadlock than a storage deadlock, and usually arises because one or more processes are consistently generating more IPs than they receive. In this kind of deadlock, giving them more storage usually doesn't help - the network just takes longer to crash. However, in the case of a loop structure like a Bill of Materials explosion, some processes are consistently generating more IPs until you reach the elementary items, so you have got to think pretty carefully about how many IPs may be in storage at the same time. When in doubt, use a file!
If all this seems a trifle worrying, in most cases you will find that you can recognize deadlock-prone network topologies just by their shape. In fact, the very shapes of the above networks constitute a clear warning sign: any loop shape in your network diagram, whether
circular
Figure16.15
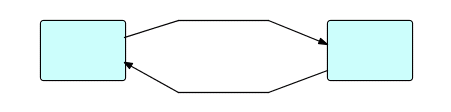
or divergent-convergent,
Figure16.16
should be treated with caution, as they are possible sources of deadlocks.
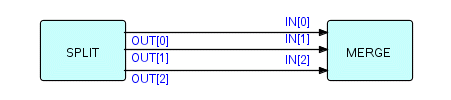
In an earlier chapter (Chapter 8), we talked about how, after you have split a stream into multiple streams, the output streams will be "decoupled" in time. If you decide you want to recombine them, you will usually land up with a variant of the above diagram. Unless you are willing to use the "first come, first served" type of merge (by connecting multiple output ports to one input port), you are creating a very fertile environment for deadlocks. Generally speaking the split and merge functions have to be complementary, but that may not be enough. Let's set up an example. Suppose we want to spread a stream of IPs across 3 servers, and then combine them afterwards. One approach might be to use a "cycling" splitter, which sends its incoming IPs to its output port elements 0 to n-1 in rotation. We will also need a merge which takes one IP from each port element in rotation and outputs them to a single output port. The picture looks like this (setting 'n' to 3):
Figure16.17
Now we can add any processing we like at the spots marked X, Y and Z. Well, not quite, as a number of people have discovered. For one thing, MERGE must see 0's, 1's and 2's in strict rotation. If you want to drop an IP, you had better make sure there is a "place-holder" IP in its place, unless you can arrange to drop one or more entire sets of 0, 1 and 2. If you don't do this, at the least your IPs will be out of order, and you may eventually get a deadlock (actually that might be better from a debugging point of view!). The same thing applies if you want to add extra IPs, except that the place-holders will have to be in the other streams. We have found that this impulse to split up streams into multiple ones is a common one among programmers, and it can be very useful. I give this example as a warning of some of the pitfalls which await you when you try to recombine them. In fact, it may not even be necessary! You may find that the assumption that data has to be kept in strict sequence is just a hold-over from the old synchronous style of thinking! [Humans usually like to see data in sort sequence, but computers often don't care!]
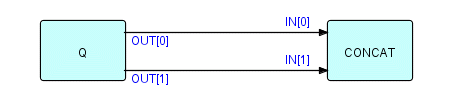
I am going to show one more deadlock example, because it illustrates the use of the "close port" service, which has been required by all FBP dialects. Consider the following diagram:
Figure16.18
You know that CONCAT receives all IPs from [0] until end of data, and then starts receiving from [1], and so on. What can you deduce about the upstream process Q? Well, it should somehow be able to generate two output streams which overlap as little as possible in time. We also notice that this (partial) network has a divergent-convergent topology, which suggests it is deadlock-prone. What might cause it to deadlock? One possibility is if Q starts to send IPs to [1] while CONCAT is still expecting data at element [0]. What causes CONCAT to switch from [0] to [1]? CONCAT switches every time it detects end of data on an input port element. But... end of data is normally caused by the upstream process terminating, and Q has not terminated. So Q has to have some way to signal end of data on [0] to CONCAT, so CONCAT can start processing the data arriving at [1] - otherwise CONCAT will still be waiting on [0] while data build up on [1]. What Q has to do is close each of its output ports before it switches to the next one. This will send a signal downstream enabling CONCAT to switch to its next input port.
I feel the example shown in Figure 16.18 is interesting as it illustrates a useful technique for subdividing a problem: what Q is really doing is subdividing its input stream into "time domains", which CONCAT can then safely recombine into a single stream. A lot of sequential files in the business world have this "time domain" kind of structure - e.g. a file might have a header portion, perhaps a list of cities followed by a list of sales staff, followed by a trailer portion. This kind of structure can be handled nicely by splitting processing into separate "time domains".