This chapter has been excerpted from the book "Flow-Based Programming: A New Approach to Application Development" (van Nostrand Reinhold, 1994), by J.Paul Morrison. A second edition (2010) is now available from CreateSpace eStore and Amazon.com. The 2nd edition is also available in e-book format from Kindle (Kindle format) and Lulu (epub format). To find out more about FBP, click on FBP.
For definitions of FBP terms, see Glossary.
|
Material from book starts here:
Up to this point, I have been talking about single IPs travelling through networks, like cars and buses in a system of highways. I have talked about how streams of IPs can be treated as higher-level entities, and how these can in turn be given more complex structures by the use of "bracket" IPs. I hope I have shown that, using these concepts, quite complex applications can be handled in a straightforward manner.
However, what if we want to build more complex structures and move them through the network as single units? Streams take time to cross a connection, and you may want a whole data structure to be sent or received at a single moment in time. Since, as we said before, only the handles travel through the net, it is just as easy for an IP containing one bit of data to be transferred from process to process as one containing a megabyte, so why not allow complex structures to move as a unit? It turned out that there was a natural analogue to this idea in real life (which always tends to reassure us that we are on the right track!). We mentioned before the idea that IPs are like memos - you can dispose of one in one of three ways: you can forward it (send), discard it (drop), or keep it (using the various methods of holding onto IPs, e.g. stacking, saving on disk, etc.). Well, of course there is a fourth thing you can do with a memo (no, not wad it up and throw it at a neighbour) - clip it to another piece of paper, and then do one of the previous three things with the resulting composite memo. Make that four things, actually, since you could clip the composite memo to another piece of paper, or to another composite memo, and so on.
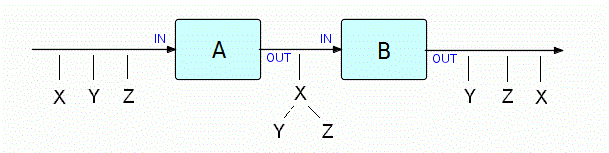
Just as the composite memo can be sent or received as a unit, so the structure of linked IPs, called a tree, can be sent or received as a single object. Once a process has received the tree, it can either "walk" it (move from IP to IP across the connecting links), completely or partially disassemble it, or destroy it. For instance, the receiver might walk the tree looking for a particular kind of IP, and, for each one it finds, it could unlink it and dispose of it in one of the standard ways. The following diagram shows two processes, one assembling trees and one disassembling them again:
Figure 12.1
A converts a series of three IPs of different types and sizes into a tree of IPs, and B disassembles the trees and outputs the component IPs (in a different order).
In all implementations of this concept so far, no node could descend from more than one parent node, and we did not allow any loops - much like a real live tree! I do not believe we lost much expressive power by doing so. The main reason for doing this is to allow FBP's ownership and disposal rules for IPs to work.
You will probably have realized that we don't need any special mechanisms as long as the tree is assembled and disassembled within one activation of one process (activation is described in detail in the chapter on Scheduling Rules). In fact you could read in a set of IPs and build an array of pointers for sorting, say - this is in fact how a number of components work. It is only when a tree has to be passed from one activation to another, or from one process to another, that the IP disposition rules have to be taken into account. Thus, in the picture above, process A receives (or creates) three IPs, assembles them into a single tree of 3 IPs and sends it out - in this case A starts with an "owned IP count" of 3, and reduces it to 0 by attaching 2 IPs to the root (count is now 1) and then sending the tree as a whole out (count of 1 goes to 0). B receives one IP (count goes from 0 to 1), and detaches the attached IPs (count goes from 1 to 3). These detached IPs must then of course be disposed of by the normal rules. If we allowed any violations of the above rules about tree shape, we wouldn't be able to map so easily between trees and streams.
In one application we had a striking example of how useful trees can be in the FBP environment: in a batch banking application, bank accounts were represented by complex sequential structures on tape. Each account record consisted of an account header, followed by a variable number of different trailer records belonging to a large number of different types, e.g. stops, holds, back items, etc. The problem was that, most of the time one could just process these sequentially, but sometimes processing later in the stream resulted in changes which should be reflected earlier in the stream. For example, an interest calculation, triggered by a particular type of trailer record, might require the account balance in the header record to be updated. You could always hold on to the header and put it out later, but then it would have to collated back into its correct position. And anyway there was quite a lot of this "direct" access going on, including adds and deletes of trailer records. Using conventional programming, this application became fiendishly complex because all the logic had to be coordinated from a timing point of view, and there were timing conflicts between when things were required and when they became available! (We know this because originally it was coded using conventional logic, and it was very complex!) We were also talking about large volumes of these structures - we had to be able to process about 5,000,000 every night. When we did this application using FBP, we realized that we could implement this application very simply and naturally by converting each sequential record into a tree structure. Once the tree had been built, "direct access" type processing could jump from one IP type to another within the tree structure, add or delete IPs, etc., and then the whole thing could be converted back to linear form when we were finished. This solution turned out to be simple to understand, easy to code and easy to maintain.
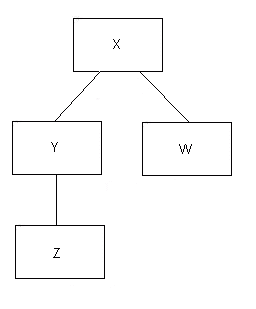
Now let's draw a picture of a simple tree of four IPs:
Figure 12.2
The top box represents the "root" IP, and all the other IPs are
descended
from it directly or indirectly. In the above diagram (mixing our
metaphors
a bit):
-
X is the root
-
Y and W are the daughters of X
-
Z is the daughter of Y
-
Z and W are leaves (terminal IPs)
-
Y is a non-terminal IP
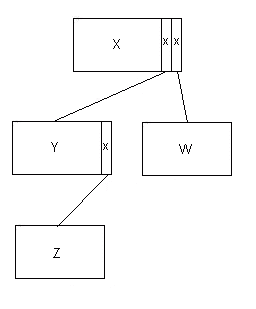
AMPS and the earlier versions of DFDM took the approach that an
attached IP required a pointer field to be specified as part of the
mother's
data. This meant that a tree structure could only be traversed using
languages
which supported pointers, e.g. PL/I, C, etc., but it did have the
advantage
that, using these languages, we did not have to have any explicit tree
traversal services. In fact, we only needed an "attach" service and a
"detach"
service. The more fundamental problem was that the layout of a given IP
had to allow for the maximum number of children that it might have -
thus,
in the above diagram, X would have to provide (at least) two pointers,
and Y one. Schematically (with the pointers shown as 'x's):
Figure 12.3
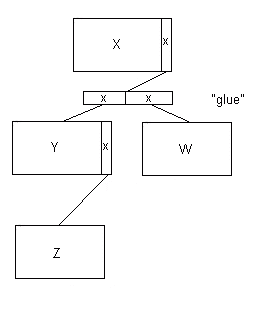
However, if Y and W could be conceptualized as a single list (rather than two different kinds of relationships) - say an employee's children, you could build "glue" IPs and use them to look after the linkage. The above diagram would then become:
Figure 12.4
Along these lines, this simple mechanism lets you build a wide variety of structures by creating special IP types which contain various arrangements of pointers. For example, you could build a chain by just adding one pointer field to each IP in the chain, which can be used for the successor IP if there is one. You could build LISP-like lists by having "car" and "cdr" pointers on each IP, or even only on certain reserved IP types ("glue"). My colleague Charles Douglas came up with the neat analogy that, when you use a paper clip to attach two memos together, the paper clip takes up some room on the paper!
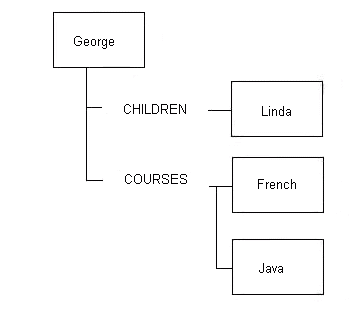
For the Japanese DFDM product, our group felt that you should not have to preplan all the list structures an IP might have attached to it. For instance, an employee might have lists attached to him or her showing children, courses attended, departments worked for, salary history, etc., and it would very nice if this information could be added incrementally, without having to change the descriptions of participating IPs. We therefore introduced the idea of named chains, any number of which could be added to an IP, without that IP requiring any changes to its description. An employee IP could for instance have the following chains attached to it: CHILDREN, SALARY_HIST, COURSES, etc. We then of course needed to provide traversal services, and we in fact built some fairly powerful services, e.g. add an IP to a named chain (it is created if it does not yet exist), get next chain (so you could walk the chains without knowing their names), get the first IP of a named chain, get next IP in a chain, detach an IP from a chain, and so forth. You could attach a chain to an IP, or an IP to a chain, but not a chain to a chain, or an IP to an IP. These trees thus had a less uniform structure (chains alternating with data IPs), but we felt that this still provided a powerful paradigm, and a less "programmer-dependent" approach to tree manipulation and traversal. An employee IP with one child, Linda, and who has taken two courses might look like this:
Figure 12.5
Along the same lines as having to dispose of IPs explicitly, we had to put certain constraints on how trees can be disassembled. This is hinted at above when we talked about "direct" and "indirect" descent. The root is owned directly by whichever process has just received it. IPs which are chained to that root are therefore owned indirectly by the same process (they are not owned directly by anyone, except possibly the root IP). You can only send or drop an IP you own directly - you have to detach a chained IP first, then send it or drop it. A process can however chain another IP (which it must own directly) onto an IP which it only owns indirectly, but that's the only service it can reference it with, apart from looking at it! We also added logic to check that a process did not try to chain a root IP onto one of its own descendants - that would have been allowed by the other rules, but would result in a closed loop!
If the above sounds complicated, try this analogy: suppose you have just cut down a tree, and you want to dispose of it. It seems reasonable that, before you burn a branch, you should cut it off first. We could arrange that burning a branch without cutting it off first would "cauterize" the point of attachment, but it seems that this would add unnecessary complexity. Conversely, we will allow you to add leaves and branches to the tree, but only if they are not connected to another one! Also, you are not allowed to attach things to a tree in such a way that part of the tree becomes a closed loop!
One other point about trees is that hierarchic tree structures, no matter how they are implemented, can easily be converted into nested substreams like the ones described in Chapter 11. For instance, the tree shown in Figure 12.2 can be "linearized" as follows:
<X <Y Z> W>
Figure 12.6
where the convention is that the IP following a left bracket is the "mother" of the other IPs at the same level of bracket nesting. This kind of transformation will be familiar to LISP users. In fact we have just shown a LISP "list of lists".
In the "chain" implementation described above, we would have to capture chain identifiers, so we can just add chain information to the left brackets, as we did in Chapter 9. Thus the tree shown in Figure 12.5 might look as follows after linearization (as in earlier chapters, the "group name" is shown as the data part of open and close bracket IPs):
IP type data
< employees
employee George
< children
child Linda
> children
< courses
course French
course COBOL
> courses
> employees
Figure 12.7
This can then easily be converted back into tree format if desired. It also of course corresponds quite well to various data base approaches: "children" and "courses" could be different segment types in an IBM DL/I data base. In IBM's DB2 we could make "employee", "children" and "courses" different tables, where "employee" is the primary key of the "employee" table, and a foreign key of the other two. [Of course this maps perfectly onto XML!]
One last point: although we have stated several times our belief that IPs should be disposed of explicitly, it turns out to be very useful to be able to discard a whole tree at a time. The tree therefore has to have enough internal "scaffolding" to allow the 'drop' service to find all the chains and attached IPs and discard them. The later versions of DFDM needed this anyway, so that they could provide services like 'locate next chain', but this ability to drop a whole tree turned out to be important even when we had no traversal services. Although at first it seemed that applications would always know enough about the tree structure to do the job themselves, we developed more and more generic components which understood about trees generally, but not about specific tree structures. This facility perhaps most closely resembles the "garbage collection" facility of object-oriented and list-oriented languages.