This chapter has been excerpted from the book "Flow-Based Programming: A New Approach to Application Development" (van Nostrand Reinhold, 1994), by J.Paul Morrison. A second edition (2010) is now available from CreateSpace eStore and Amazon.com. The 2nd edition is also available in e-book format from Kindle (Kindle format) and Lulu (epub format). To find out more about FBP, click on FBP.
For definitions of FBP terms, see Glossary.
|
[References to TR1 in the text refer to an application component which is used in examples earlier in the book - see Chapter 10. TR1 "extends" detail records by multiplying a quantity in a detail record by a unit price obtained from a master record in another file. Processes "up-stream" of TR1 have merged masters and details, so TR1 is fed a single merged stream containing masters and details, and with related records delimited by special IPs called "brackets".]
Material from book starts here:
It has been noted by several writers that there seems to be a good match between compiler theory and the theory of sequential processes. FBP processes can be regarded as parsers of their input streams.
The component labelled TR1 in the example in Chapter 10 can be considered as a "parser", while the structure of its input stream can be specified using a syntactic form called a regular expression. This allows a number of the concepts of modern compiler theory to be applied to it. Let us express the input stream of component TR1 in that application as a "regular expression", as follows:
{ ( m d* ) }*
which can be read as:
zero or more groups of:
one open bracket,
one master IP (m),
zero or more details (d),
one close bracket
(In what follows, I will use brackets to represent bracket IPs, and curly braces will have syntactic meanings.)
Each of TR1's output streams consists of repeating strings of identical IPs. Representing modified masters as m', extended details as d' and summaries as s, we get the following "regular expressions" for the three output streams:
m'*
d'*
s*
Each of these output streams has a well-defined relationship with the input stream, and it would be very nice if some notation could be developed to show this relationship clearly and concisely. In fact, this would constitute a complete description of what TR1 does: a component's function is completely described by its input and output streams, and the relationships between them.
In Aho and Ullman's 1972 book they show that a regular expression can be parsed by a deterministic one-way finite automaton with one tape, usually referred to simply as a "finite automaton". This tape contains "frames", usually containing characters, but in what follows we shall think of the frames as containing entire IPs. As each frame is scanned, the automaton may or may not change state, and may or may not perform an "action", such as reading or writing a frame. Whether or not there is an action, the tape continues moving.
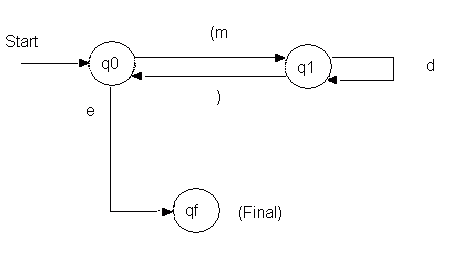
A convenient way to represent the various state changes is by means of a "Transition Graph", where each node represents a state, and each arc represents a transition from one state to another (or from a state to itself), and is marked with the name of the IP being scanned off, as follows:
Figure 24.1
In these diagrams, e is used to indicate the "end of data" condition; m, d, ( and ) represent masters, details, open and close brackets, respectively. Since an open bracket is always followed by a master in this example, I have shown them combined on a single transition arc.
An alternative to the transition graph is the "State Table". This uses a tabular format, which is often more convenient. The following table is equivalent to the preceding diagram.
State Input | New State
------------|-------------
q0 (m | q1
q0 e | qf
|
q1 d | q1
q1 ) | q0
|
qf | Final State
Figure 24.2
Aho and Ullman next show that any regular expression may be described by a right linear grammar, expressed as a series of productions, each of which describes a pattern in terms of the sub-patterns or final symbols which make it up.
Productions can be understood in a generative sense - i.e. all legal streams can be generated by successively taking choices from the set of productions, starting with S. Alternatively, productions can be used to describe relationships between patterns being scanned off by a parser.
A grammar is called "right linear" if patterns on the right-hand
side may
only occur at the end of a production. Here is a right linear grammar
which
is equivalent to the "regular expression" given above, using the
notation
of productions, but using lower-case letters to represent IP types, as
in
the state diagram above. ![]() means a null stream.
means a null stream.
S ->
S -> (mR
R -> )S
R -> dR
where the two lines starting with S indicate two patterns which both constitute valid S's, and similarly for the two lines starting with R.
Since lower-case letters in the productions represent objects that cannot be parsed further (i.e. IPs), upper-case letters may be thought of as representing expectations or hypotheses. Thus R in the above productions represents "that part of a stream which can follow a master or detail". Thus, when a master is detected, the automaton's expectation of what may follow changes from what it was at the beginning of the stream, and, when a close bracket is detected, it changes back. This exactly mirrors the state changes of the finite automaton shown above.
While the right linear grammar shown above adequately represents the automaton traversing the stream one IP at a time, it cannot "see" patterns which consist of more than one IP, and therefore cannot express one's intuitive feeling for the hierarchic structure of the IP stream. For this we must go to a more powerful class of grammar, called the context-free grammars.
The set of context-free grammars (CFGs) is a superset of the set of right linear grammars, in that a pattern symbol is allowed to occur anywhere on the righthand side of a production. Since CFGs are more general than right linear grammars, they require a more complex type of automaton to process them: the "pushdown automaton" (PDA), which has, in addition to its input tape, memory in the form of a "pushdown stack". This may be thought of as containing subgoals or hypotheses established during stream processing, to be verified or discarded.
The following set of productions of a context-free grammar is also equivalent to the regular expression given above:
S ->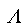
S -> AS
A -> (mT
T -> )
T -> dT
where you will notice that pattern A appears at the beginning of the right-hand side of the second production. The first two productions together can therefore be read as follows: a stream consists of zero or more A patterns (or substreams).
A pushdown automaton will have "stack states" in addition to "automaton states": in this example the automaton state is trivial, as there is really only a "normal" state (q0) and a "final" state (qf), to enable the automaton to stop.
In the following diagram, Q means "automaton state" and S is the "stack state" ( - means empty, and x means that there is an x at the top of the stack). It will be noticed that "push" and "pop" change the "stack state" in the same pattern we saw in connection with the "automaton state" in the Transition Graph shown above. Q' and S' mean the new states of the automaton and the stack respectively.
Q S Input | Action Q' S'
---------------|-----------------------
q0 - (m | push A q0 A
q0 A ) | pop A q0 -
q0 A d | pop A/ q0 A
| push A
|
q0 - e | - qf -
|
qf | Final State
The actions denoted
push x
pop x
are to be read as "push IP x onto stack," and "pop IP x from stack," respectively.
Figure 24.3
You will recognize that this use of the stack exactly parallels the use of a stack in FBP to hold IPs being worked on.
In FBP we restrict the use of the stack as follows: while an IP is in the stack, it is not available for use by the component's logic. It must therefore be "popped" off the stack to make it available for processing. At the end of processing, it must be explicitly disposed of before the automaton leaves that state, either by being returned to the stack, or by being sent or dropped. This is the reason for the pop/push combination - if we weren't using an FBP implementation, we could leave it out altogether, as it leaves the stack state unchanged, but in FBP it is required in order to make A available for processing.
It can be seen from the above that the only function of the state Q is to determine when the automaton has reached a final state - the rest of the time the automaton is in its normal state. The two states of the stack correspond one-to-one with the states q0 and q1 in the non-pushdown automaton, so that the stack has a dual function: that of storage for IPs being worked on, and control. This exactly mirrors the way FBP uses a stack for holding control IPs. The process of stacking a subgoal which represents a substream corresponds to the FBP concept of stacking an IP to denote the entire substream.
Where do we go from here? There has been quite a lot of work on describing applications using PDAs, but I am not aware of much work tying them together with data streams (I would appreciate hearing about such work). This seems to me a fruitful direction for more research, and may yield new ways of looking at applications, or even new hardware designs.